GPU-Puzzles全记录

前言

某天在知乎上刷到了一个很有意思的GPU并行编程学习仓库，叫GPU-Puzzles，通过解谜+可视化的方式学习并行编程，使用Python就可以实现CUDA核函数，并且可以观察线程和数据的对应关系，对于初学者而言非常友好。仓库链接，花了一个下午全部解出来了，以下记录下我的题解和对于题目的分析理解。

题解

Puzzle 1

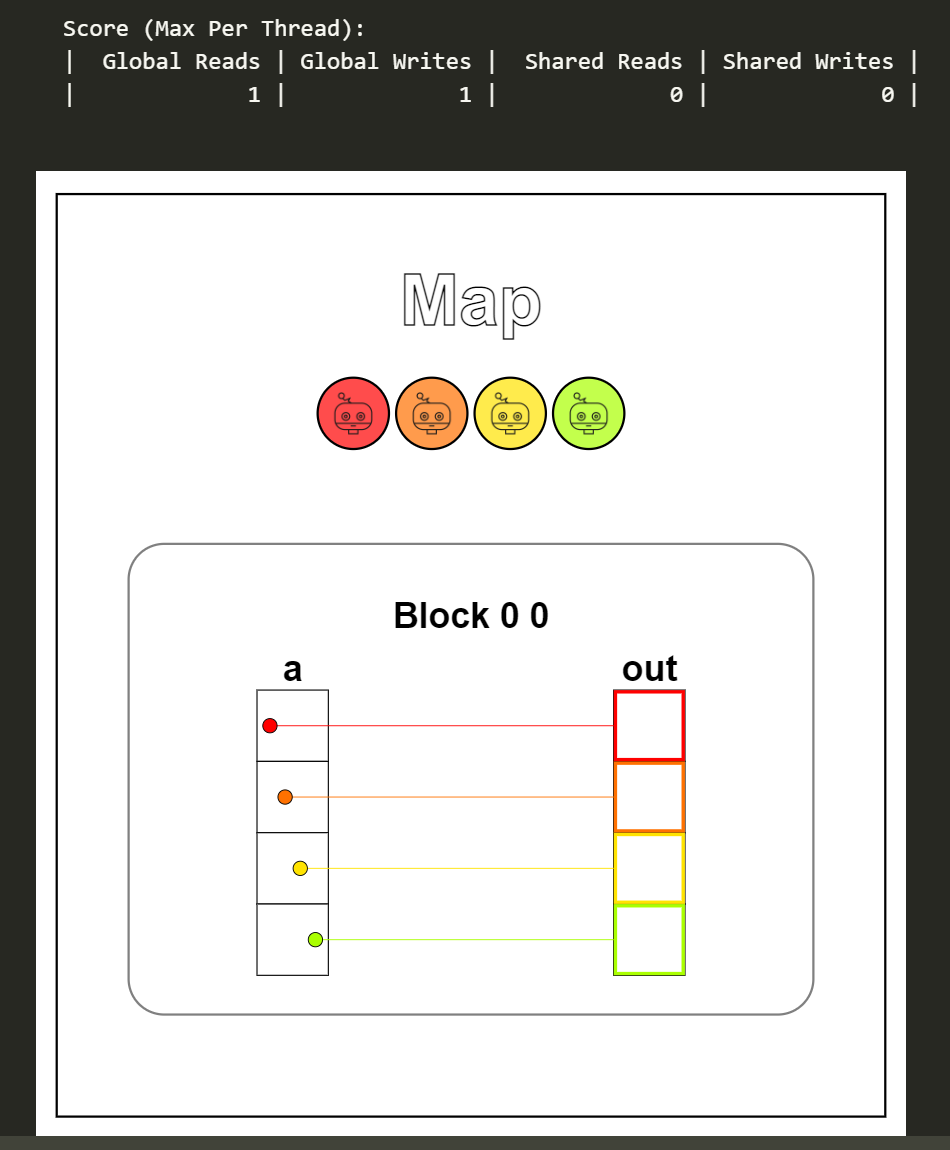
题目：Map。签到题，顾名思义就是映射，题目保证线程数量与数据量一致，因此数据与线程是一对一的关系，一条线程对应处理一个数据即可。

def map_test(cuda):
    def call(out, a) -> None:
        # 通过threadIdx.x获取本Block内的线程号
        local_i = cuda.threadIdx.x
        # 直接+10，写回到输出的对应位置即可
        out[local_i] = a[local_i] + 10
    return call

下图便是本题的可视化结果，可以看到每一条线程从数组a中读取一个数据，+10后写到out数组中，完成映射操作，全局内存上读和写的次数是一样的。

Puzzle 2

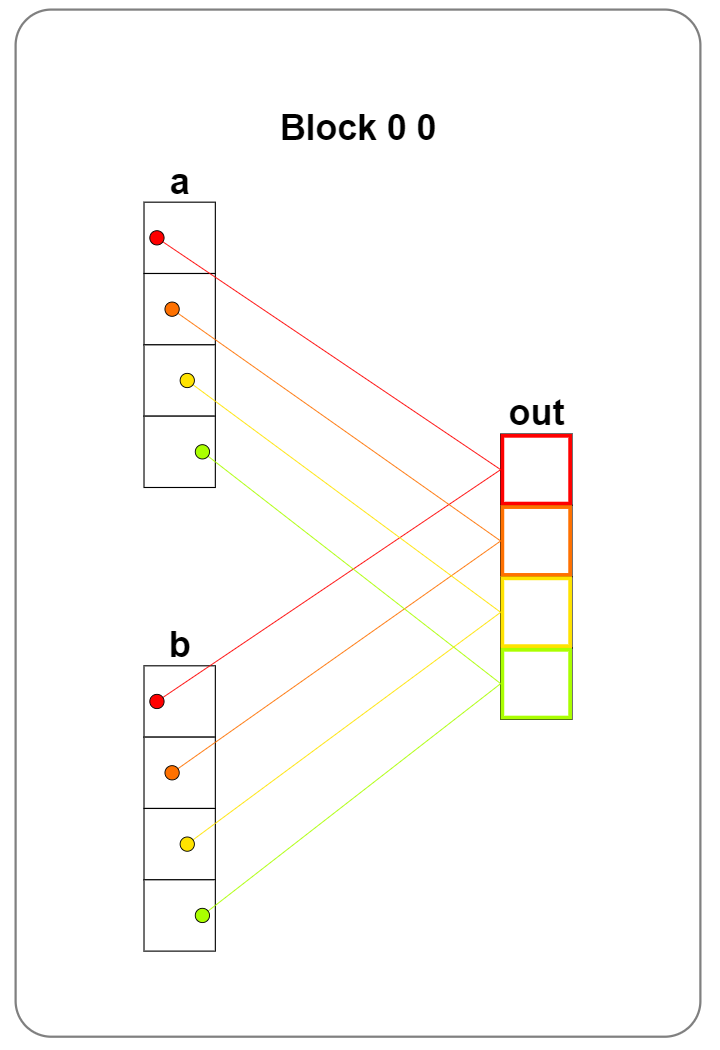
题目：Zip。可以理解为组合，将数组a和b中每一个元素相加，结果储存在out中，题目保证线程数量与数据量一致，因此数据与线程仍然是一对一的关系。

def zip_test(cuda):
    def call(out, a, b) -> None:
        local_i = cuda.threadIdx.x
        # 一对一映射关系，一条线程处理一次加法操作
        out[local_i] = a[local_i] + b[local_i]
    return call

从可视化结果可以看到一条线程分别从a和b中读取一个数据，相加后写到out中，全局内存上读的次数是写的两倍。

Puzzle 3

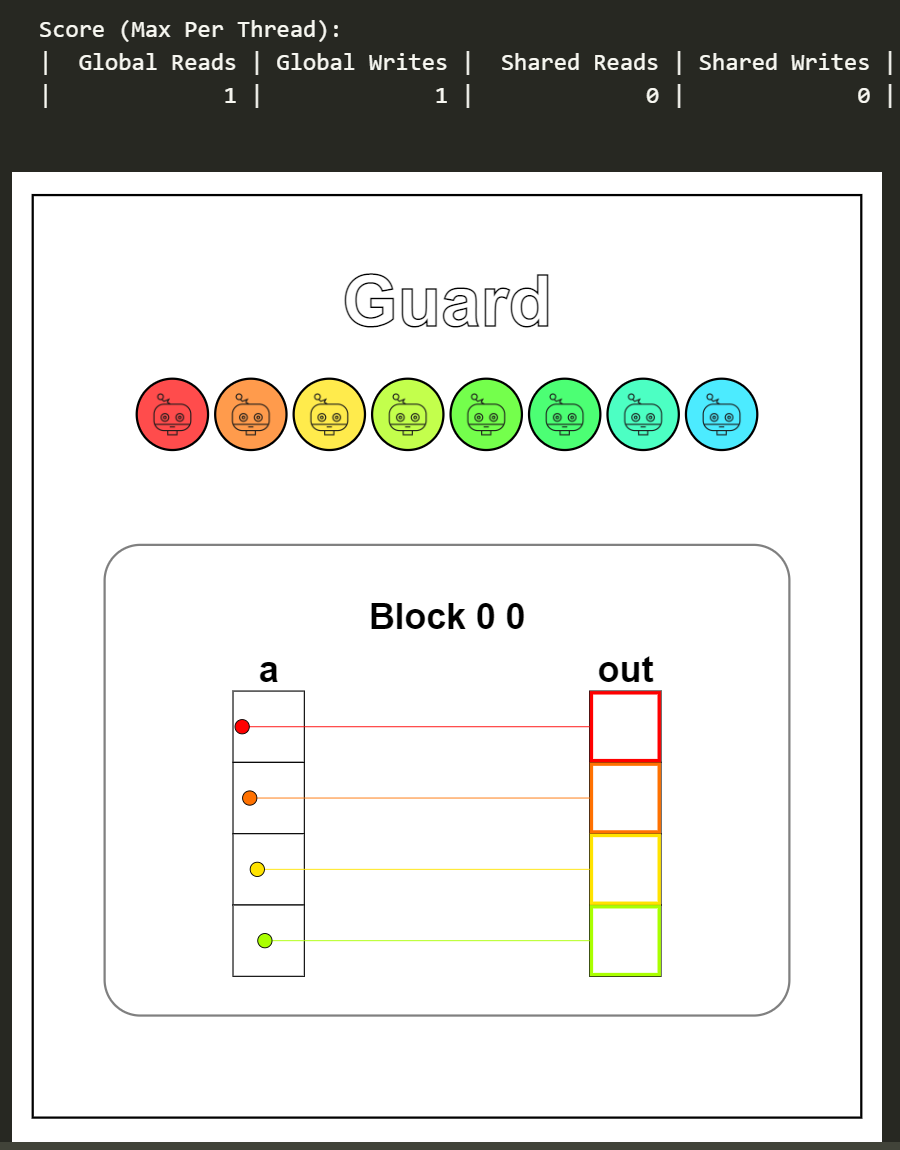
题目：Guard。从这题开始，题目就更符合并行编程下实际的情景了，线程的数量一般情况下是与数据量不相等的，在读写操作前，我们需要判断某条线程是否需要进行读写操作，以防出现越界或重复计算等错误。

def map_guard_test(cuda):
    def call(out, a, size) -> None:
        local_i = cuda.threadIdx.x
        # 当线程数多于要处理的数据量时，需要判断一下本线程是否需要处理数据
        if local_i < size:
            out[local_i] = a[local_i] + 10
    return call

这题的可视化结果看不出if local_i < size:判断有什么作用，实际上线程的数量是要多于数据量的，多出的这部分线程没有进行任何的操作。

Puzzle 4

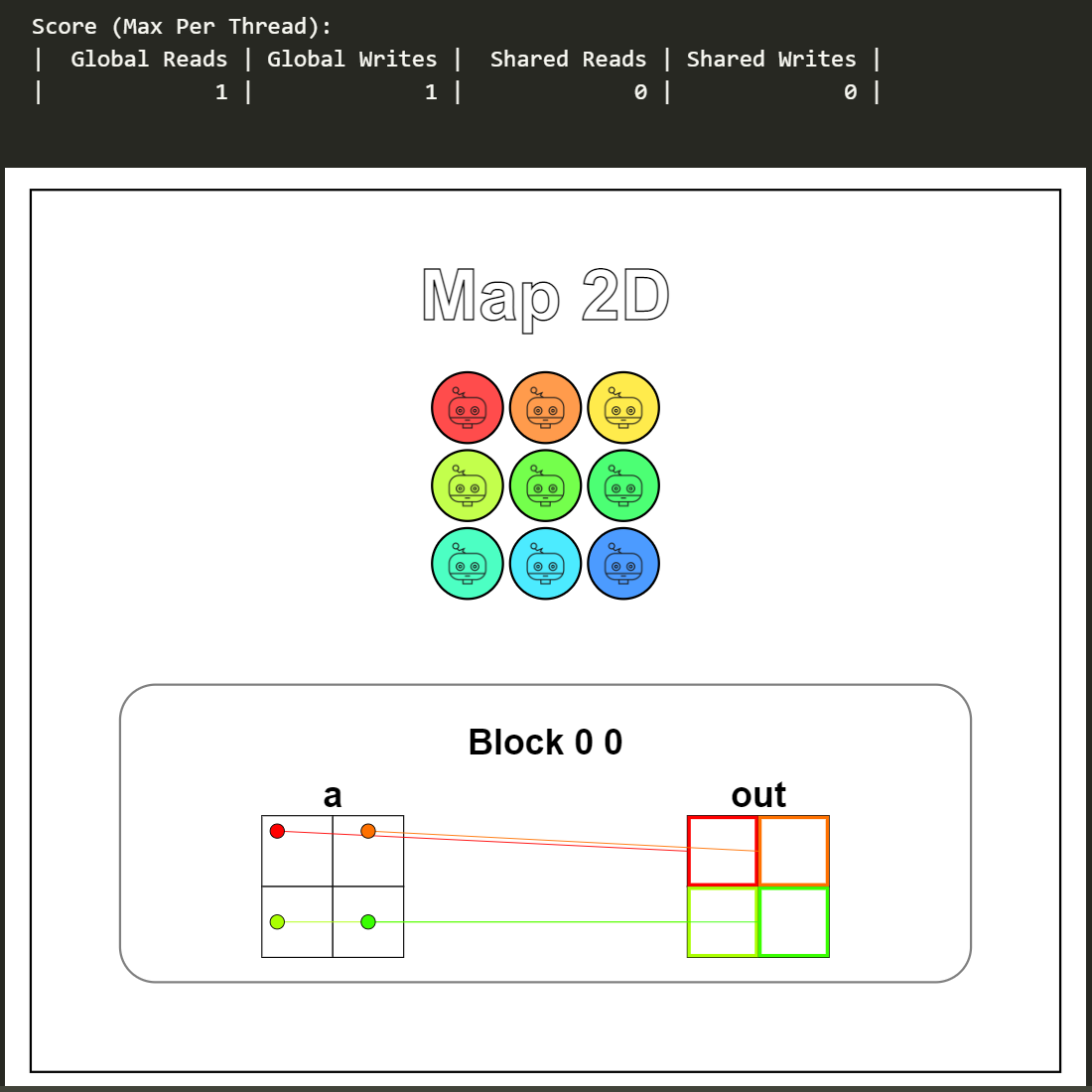
题目：Map 2D。本题是第一题的二维扩展版，在CUDA编程中，一个Grid可以有3维Block，一个Block可以有3维Thread。当启动核函数配置为多维Block或多维Thread时，我们需要稍微修改一下线程的索引方式。

def map_2D_test(cuda):
    def call(out, a, size) -> None:
        local_i = cuda.threadIdx.x
        local_j = cuda.threadIdx.y
        # 一维Block，二维Thread，按照二维数组的方式去索引即可，注意线程数量比数据量多
        if local_i < size and local_j < size:
            out[local_i, local_j] = a[local_i, local_j] + 10
    return call

从可视化结果可以看到，一条线程对应二维数组上的一个数据，同样的，没有参与数据读写操作的线程并没有画出来。

Puzzle 5

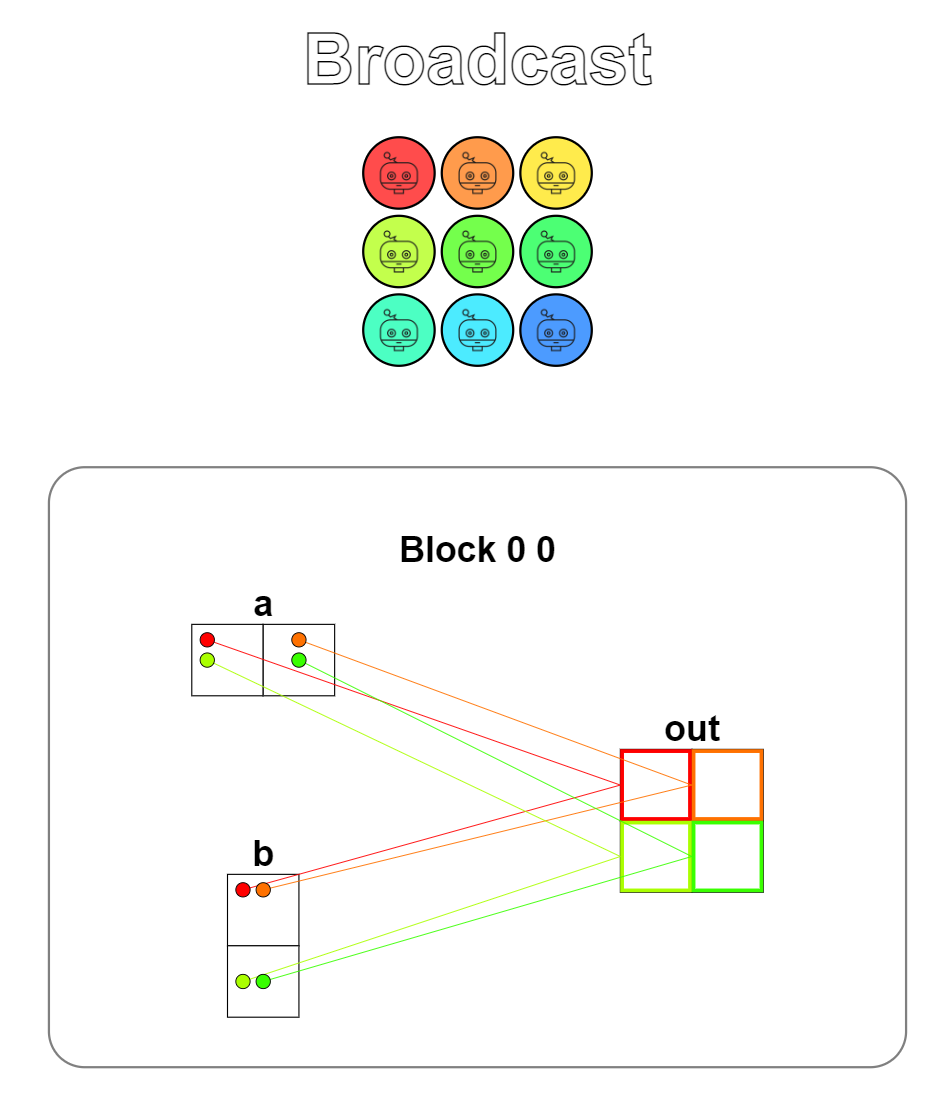
题目：Broadcast。广播操作，一个列向量与一个行向量相加，结果将会自动广播为一个矩阵，本题用了二维的Thread，注意行、列向量是一维的，需要理解输入输出数据的映射关系。

def broadcast_test(cuda):
    def call(out, a, b, size) -> None:
        local_i = cuda.threadIdx.x
        local_j = cuda.threadIdx.y
        # 广播操作，列向量 + 行向量，结果广播为矩阵
        if local_i < size and local_j < size:
            out[local_i, local_j] = a[local_i, 0] + b[0, local_j]
    return call

可视化结果如下，行向量数据映射到矩阵中的每一行，列向量数据映射到矩阵中的每一列。

Puzzle 6

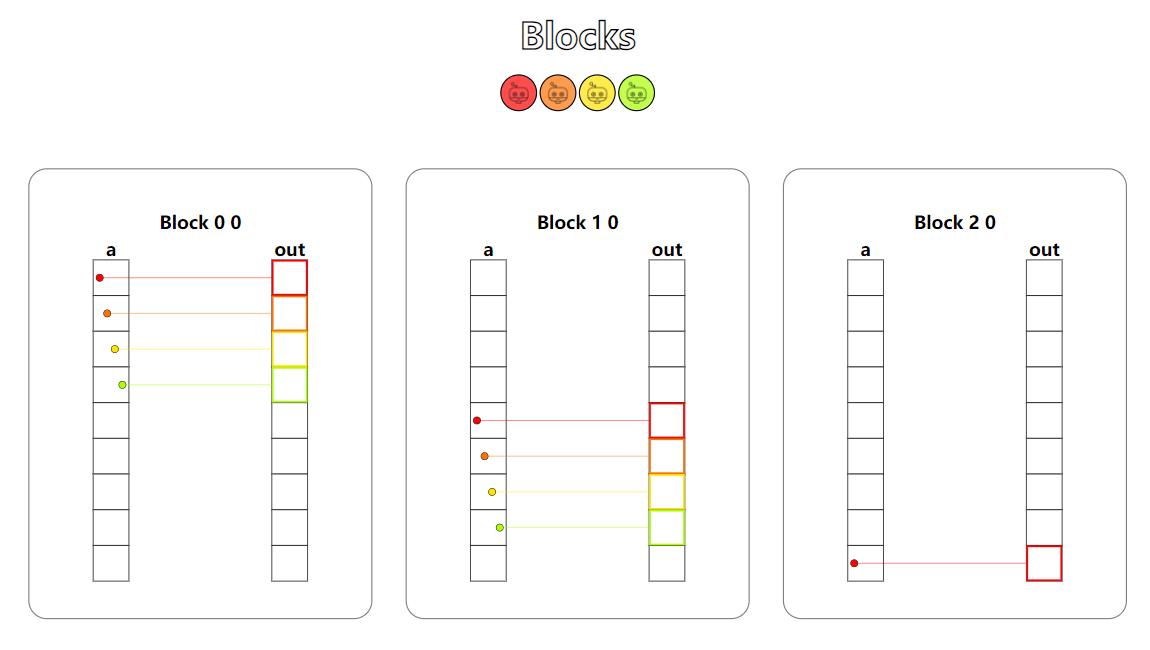
题目：Blocks。在CUDA中，每一个Block内线程的数量是有限制的，为了使用更多的线程，我们可以增加更多的Block。本题开始，核函数不再只使用一个Block了，此时我们需要考虑数据在Block间的跨度和Block内线程对数据的索引关系。

def map_block_test(cuda):
    def call(out, a, size) -> None:
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        # 多Block下的数据索引，需要考虑BlockIdx
        if i < size:
            out[i] = a[i] + 10
    return call

从可视化结果中看到，我们有多个Block，每个Block中都有相同数量的线程。考虑数据索引时，我们需要将Block间的索引也考虑上，与二维数组的索引相似，Block和Thread组成了二维的索引关系。

Puzzle 7

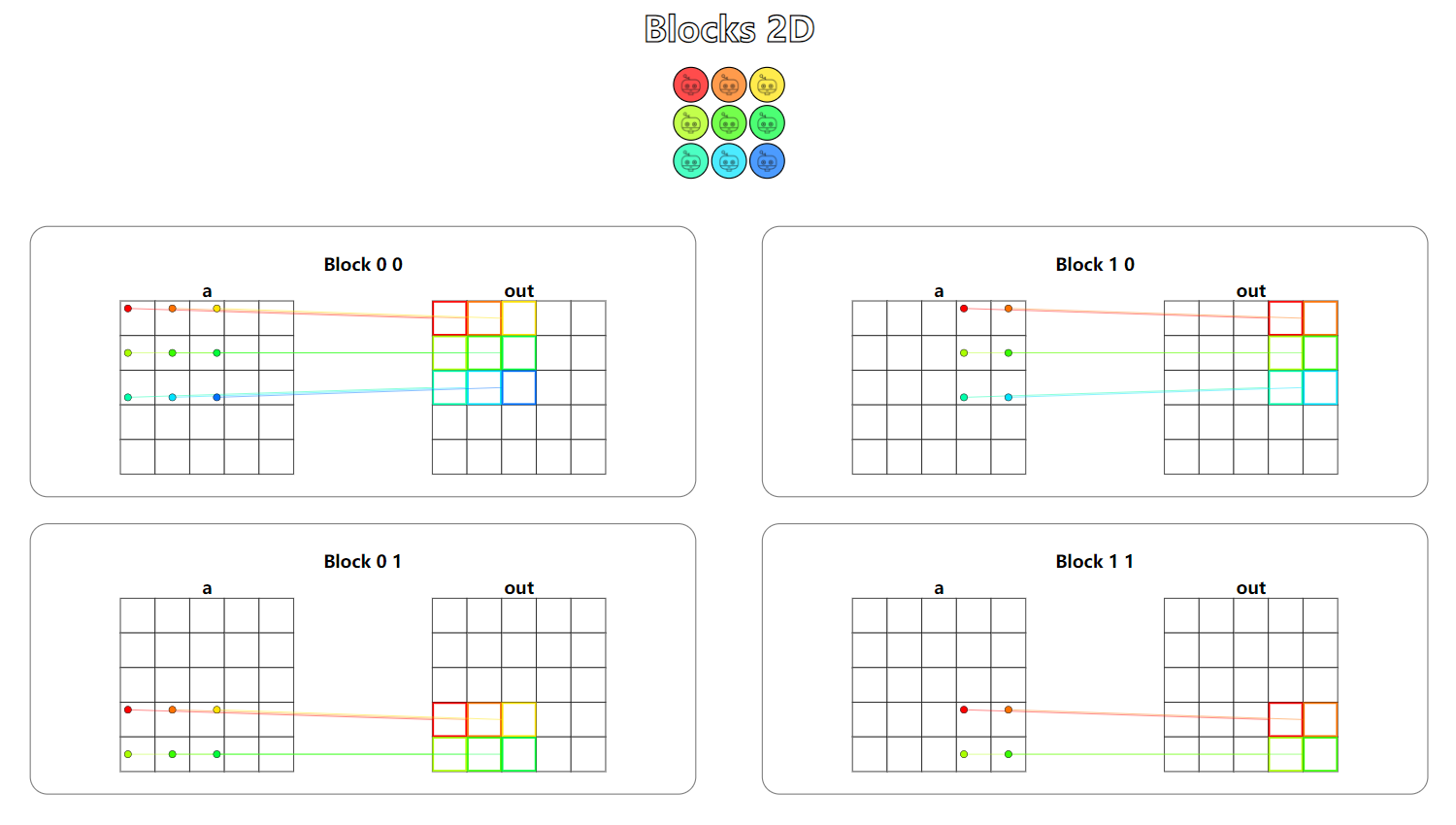
题目：Blocks 2D。二维的Block加上二维的Thread，这是实际应用中最常见的场景。

def map_block2D_test(cuda):
    def call(out, a, size) -> None:
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        # 二维多Block索引
        j = cuda.blockIdx.y * cuda.blockDim.y + cuda.threadIdx.y
        if i < size and j < size:
            out[i, j] = a[i, j] + 10
    return call

从可视化结果中可以看到，每一个Block负责处理矩阵a中的一部分数据，一个大矩阵就这样被切分为几个小矩阵，分别进行数据操作，最后写回到输出中。

Puzzle 8

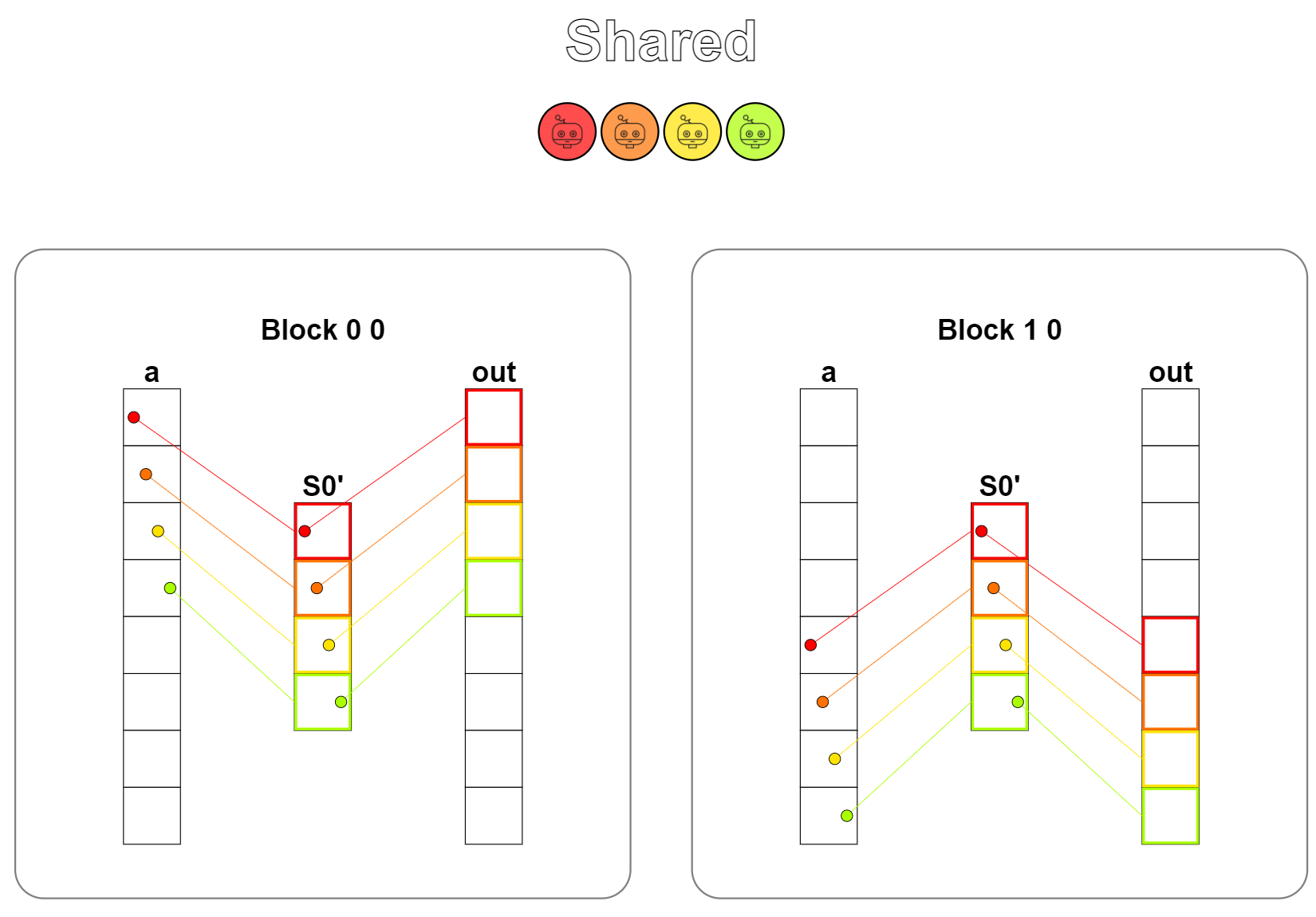
题目：Shared。本题是Shared memory(共享内存)的第一次使用，共享内存是SM中的片上内存，实际上是开放给开发人员自由编程的一种L1缓存，读写的速度要比全局内存快很多倍，当核函数需要频繁、重复地读取一部分数据进行运算时，先将这一部分数据从全局内存中读取到共享内存中，能够提升非常多倍的性能。

本题其实不用共享内存也可以，只是给大伙演示一下共享内存是如何使用的。

使用共享内存的操作一般为：从全局内存中读取数据并储存到共享内存中，显示地同步内存，保证所需的数据已正确存放到共享内存中，从共享内存中读取数据并进行计算，将结果写回到全局内存的输出中。

# Thread Per Block
TPB = 4
def shared_test(cuda):
    def call(out, a, size) -> None:
        # 声明共享内存以及共享内存的大小，注意L1缓存大小有限，不能用太大的共享内存
        shared = cuda.shared.array(TPB, numba.float32)
        # 数据全局索引
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        # 数据在Block内的局部索引
        local_i = cuda.threadIdx.x
        # 带共享内存的加法，通常操作是：从全局内存中读数据到共享内存、在共享内存上运算、将结果从共享内存写回全局内存
        if i < size:
            # 将数据从全局内存中加载到共享内存，注意是全局索引 -> 局部索引
            shared[local_i] = a[i]
            # 显式同步所有线程，保证所有数据都加载到共享内存中
            cuda.syncthreads()
            # 读写共享内存
            shared[local_i] = shared[local_i] + 10
            # 将结果写回到全局内存的输出中，此时便是局部索引 -> 全局索引
            out[i] = shared[local_i]

    return call

从可视化结果中看到，存在一个数据从全局内存中加载到共享内存上的一个操作，计算完成后将结果写回到全局内存的输出中。

Puzzle 9

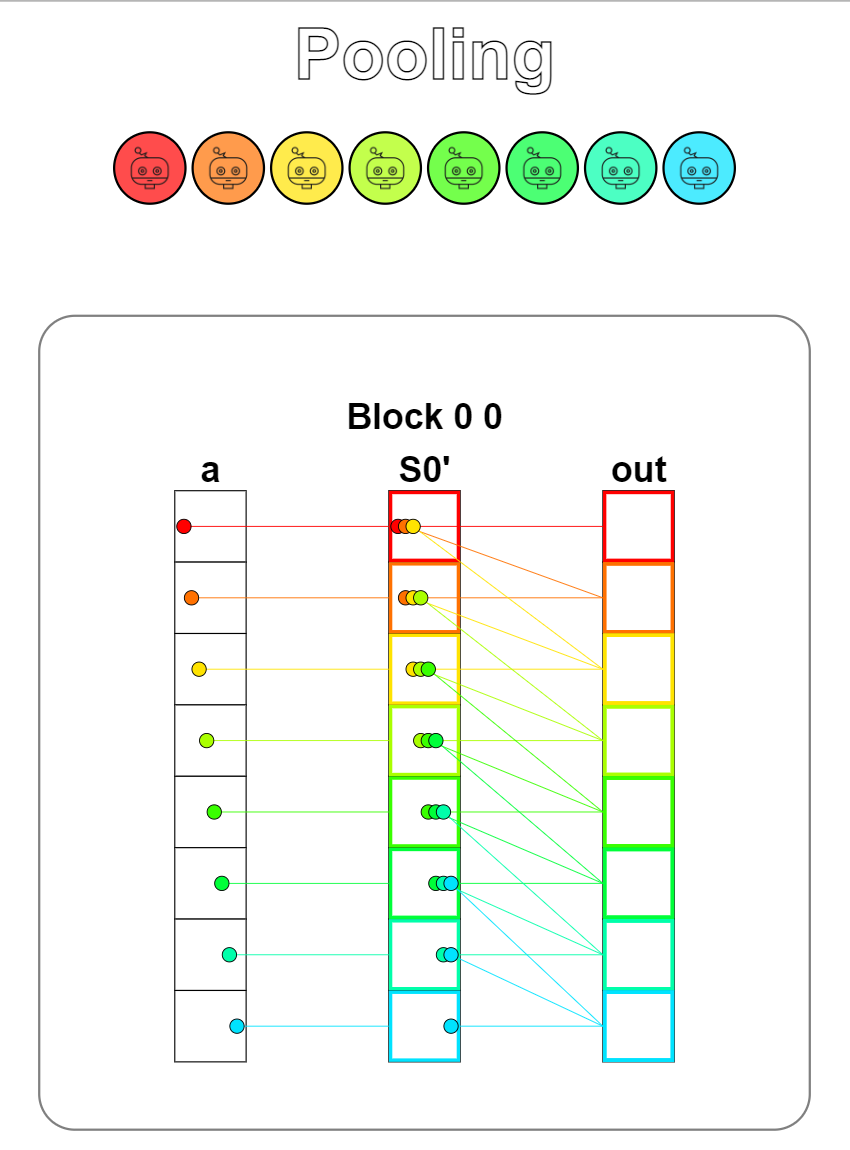
题目：Pooling。一维池化操作，池化核大小为3，需要将数组上相邻的三个元素相加，因此需要频繁地读取数据，此时使用共享内存就很有必要了。题目给的共享内存大小正好能将输入的数组a完全装下，将输入完全搬运到共享内存上后，每条线程将其相邻的三个元素相加，将结果写回输出即可。

TPB = 8
def pool_test(cuda):
    def call(out, a, size) -> None:
        shared = cuda.shared.array(TPB, numba.float32)
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        local_i = cuda.threadIdx.x
        # 模拟池化操作，池化核大小为3
        if i < size:
            # 将所有输入数据搬运到共享内存上
            shared[i] = a[i]
            cuda.syncthreads()
            # 使用一个寄存器变量，储存相加结果
            acc = 0
            # 池化核大小，注意要判断是否越界
            for j in range(3):
                if local_i - j >= 0:
                    acc = acc + shared[local_i - j]
            # 结果写回全局内存
            out[i] = acc
    return call

从可视化结果中可以看到，读取数据的次数远多于写入数据的次数，使用共享内存能带来非常大的性能提升。同时共享内存大小能装下数组a，省去了判断数据是否存在于共享内存中的判断。

Puzzle 10

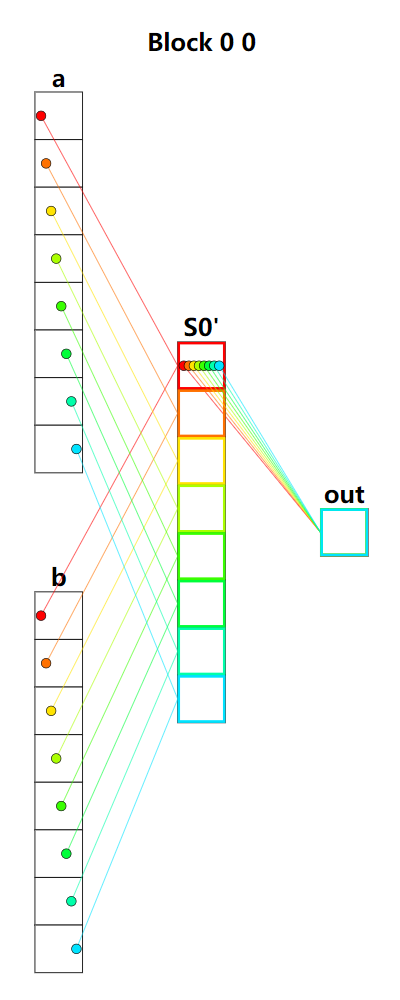
题目：Dot product。点乘，将向量a和b中对应位置元素相乘，最后相加。整体运算可以分为两个阶段，第一阶段是元素相乘，可以将数据加载到共享内存上的同时完成相乘的操作，第二阶段是元素的规约运算，将共享内存上的所有元素进行规约相加，也就是reduce_sum。

TPB = 8
def dot_test(cuda):
    def call(out, a, b, size) -> None:
        shared = cuda.shared.array(TPB, numba.float32)
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        local_i = cuda.threadIdx.x
        # 点乘，最后求和，求和部分可以用reduce解决
        if i < size:
            # 加载数据的同时进行乘法操作
            shared[local_i] = a[i] * b[i]
            cuda.syncthreads()
        # 规约求和运算，每次都是前半部分+后半部分
        stride = size // 2
        while stride != 0:
            if local_i < stride:
                shared[local_i] = shared[local_i] + shared[local_i + stride]
            stride = stride // 2
        # 写回结果
        out[0] = shared[0]
    return call

可视化结果看不出数据读写的顺序，首先是从数组a和b中读出元素相乘，并存放到共享内存中，然后将共享内存上所有元素规约相加到共享内存的第一个元素中，最后将结果写回到输出。

Puzzle 11

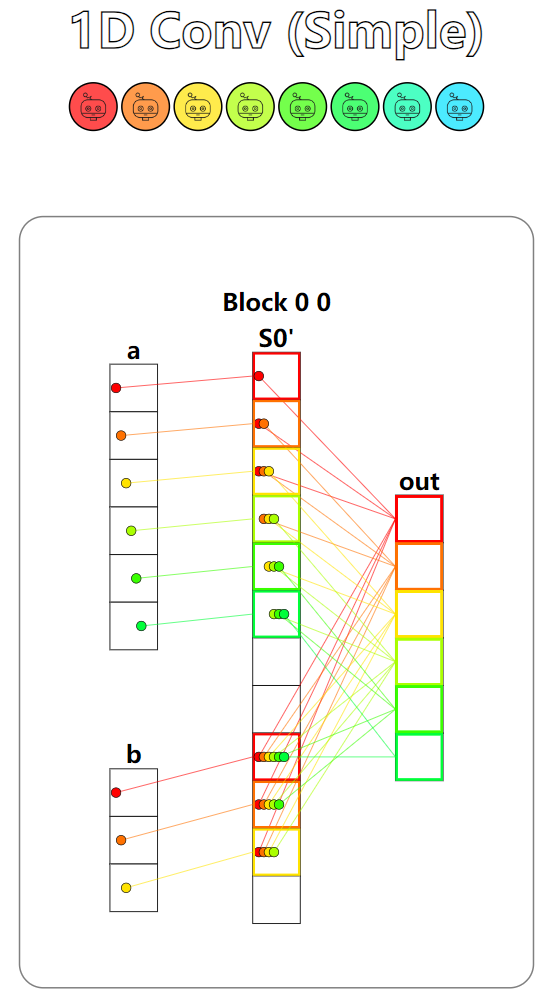
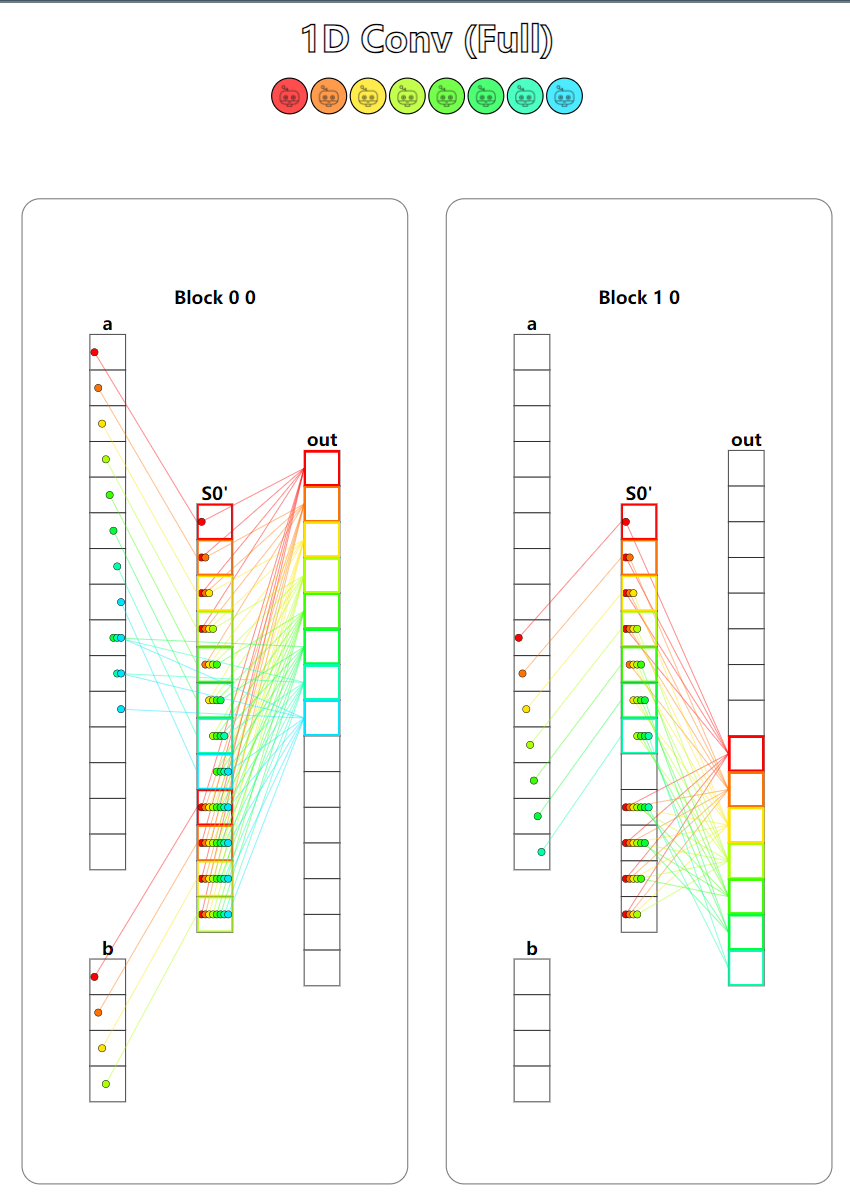
题目：1D Convolution。一维卷积运算，本题中的共享内存大小不足以存放下输入的所有元素，因此我们需要判断数据是否在共享内存上，对于不在共享内存上的数据，我们只能从全局内存中读取并计算。

MAX_CONV = 4
TPB = 8
TPB_MAX_CONV = TPB + MAX_CONV
def conv_test(cuda):
    def call(out, a, b, a_size, b_size) -> None:
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        local_i = cuda.threadIdx.x
        shared = cuda.shared.array(TPB_MAX_CONV, numba.float32)
        # 将卷积核`b`从全局内存搬到共享内存，这里保证共享内存能够放下卷积核的所有数据
        # 将卷积核的数据存放在共享内存的最后面，由于还需要将部分输入`a`的数据搬运到共享内存，这里可以省一次线程同步
        if i < b_size:
            shared[local_i + TPB] = b[i]
        # 计算`a`中每个元素对卷积核`b`的点乘
        if i < a_size:
            # 先将`a`中数据从全局内存搬到共享内存，并同步一次所有线程
            shared[local_i] = a[i]
            cuda.syncthreads()
            # 记录该点的类加值
            acc = 0
            # 对卷积核`b`进行点乘
            for j in range(b_size):
                # 记得限制一下卷积的范围，不要越界
                if i + j < a_size:
                    # 如果`a`中的数据在共享内存中有，则直接从共享内存中读，没有则从全局内存中读
                    if local_i + j < TPB:
                        acc = acc + shared[local_i + j] * shared[TPB + j]
                    else:
                        acc = acc + a[i + j] * shared[TPB + j]
            # 结果写回到全局内存中
            out[i] = acc

    return call

本题有两个测试用例，第一个测试用例只使用了一个Block，并且输入和卷积核都能够全部载入到共享内存中。第二个测试用例使用了2个Block，并且输入并不能完全载入到共享内存中。

Puzzle 12

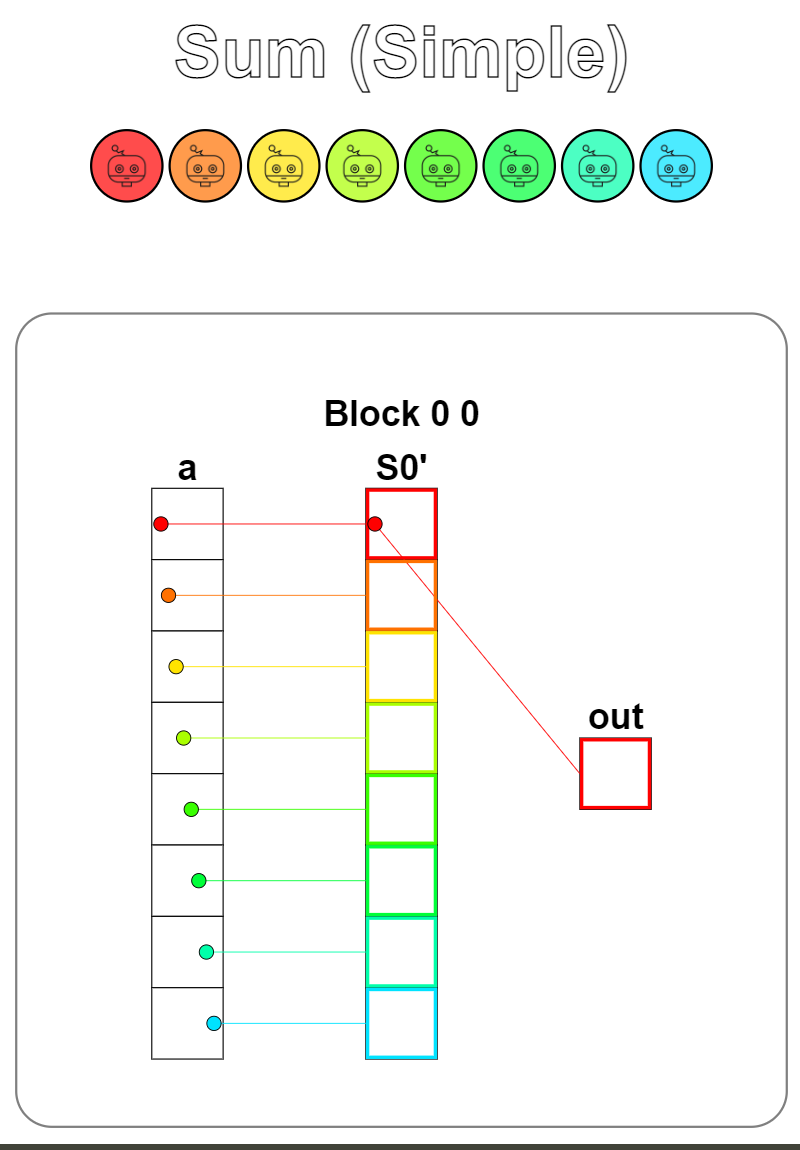
题目：Prefix sum。前缀和，其实就是规约求和，题目要求的是相邻线程相加，与第十题中使用到的规约计算方法稍有不同，相邻线程相加的情况下stride是从小到大增长的。

TPB = 8
def sum_test(cuda):
    def call(out, a, size: int) -> None:
        cache = cuda.shared.array(TPB, numba.float32)
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        local_i = cuda.threadIdx.x
        # 前缀和，其实就是reduce操作，这里实现的版本是相邻线程相加的reduce
        # 将输入加载到共享内存中
        if i < size:
            cache[local_i] = a[i]
            cuda.syncthreads()
        # 相邻线程相加
        stride = 1
        while stride != TPB:
            if local_i % (stride * 2) == 0:
                cache[local_i] = cache[local_i] + cache[local_i + stride]
            stride = stride * 2
        # 结果储存在共享内存的第一个元素中
        if local_i == 0:
            out[cuda.blockIdx.x] = cache[0]

    return call

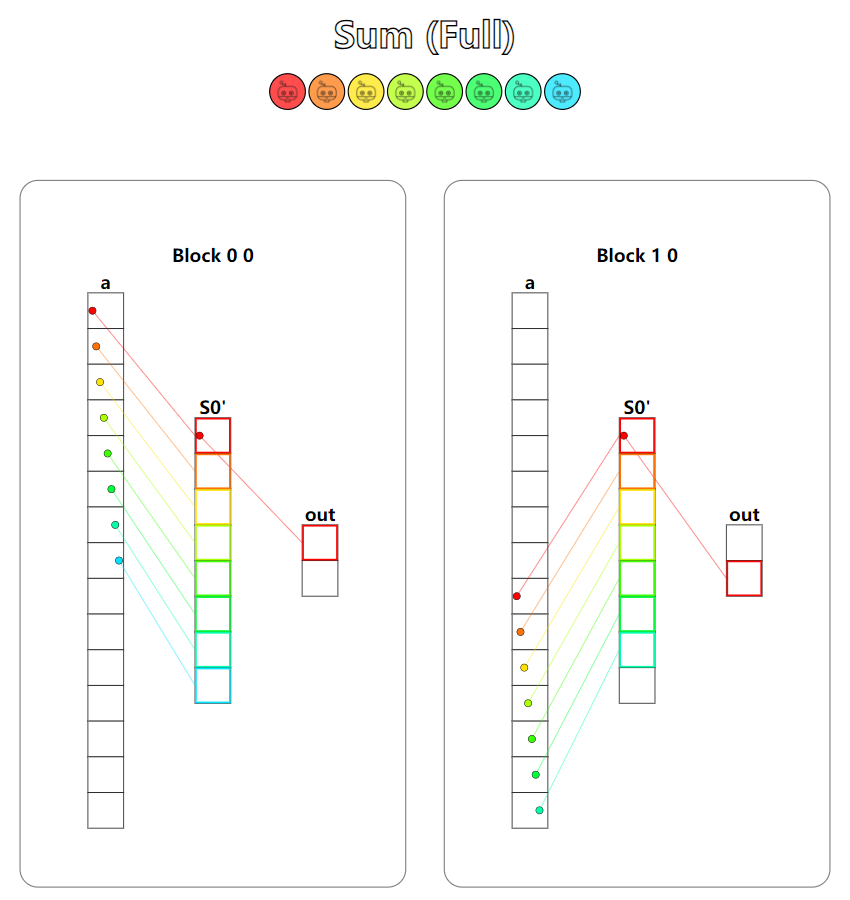
可视化图并看不出共享内存中的规约操作，图个乐就好。第二个测试用例中的输出如果要进一步求和，可以再进行一次规约操作，也称为两阶段式的reduce。

Puzzle 13

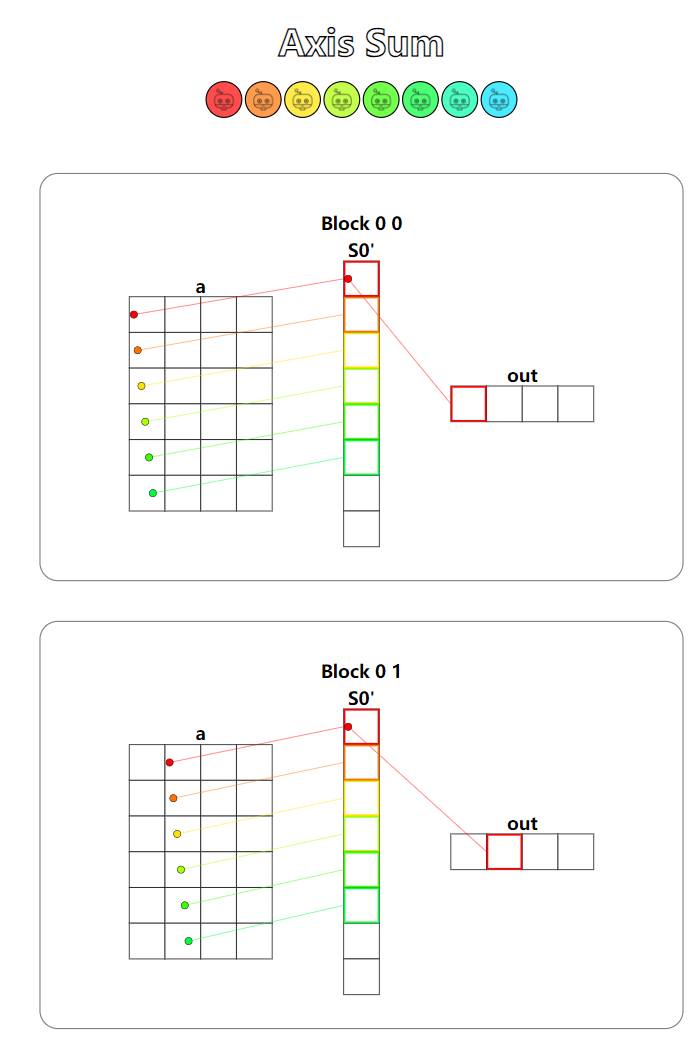
题目：Axis sum。同样是reduce_sum，不过本题支持的是任意轴上的规约操作，不同的地方在于要正确处理输入加载到共享内存上的下标映射关系。

TPB = 8
def axis_sum_test(cuda):
    def call(out, a, size: int) -> None:
        cache = cuda.shared.array(TPB, numba.float32)
        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        local_i = cuda.threadIdx.x
        batch = cuda.blockIdx.y
        # 沿某个轴上的相加操作，正确处理好batch的关系即可，其他跟reduce一样
        if i < size:
            cache[local_i] = a[batch, i]
            cuda.syncthreads()
        stride = TPB // 2
        while stride > 0:
            if local_i < stride:
                cache[local_i] = cache[local_i] + cache[local_i + stride]
            stride = stride // 2
        if local_i == 0:
            out[batch, 0] = cache[0]

    return call

可视化图太长了，截图不完全，其实与上一题多Block下的规约计算是一样的。

Puzzle 14

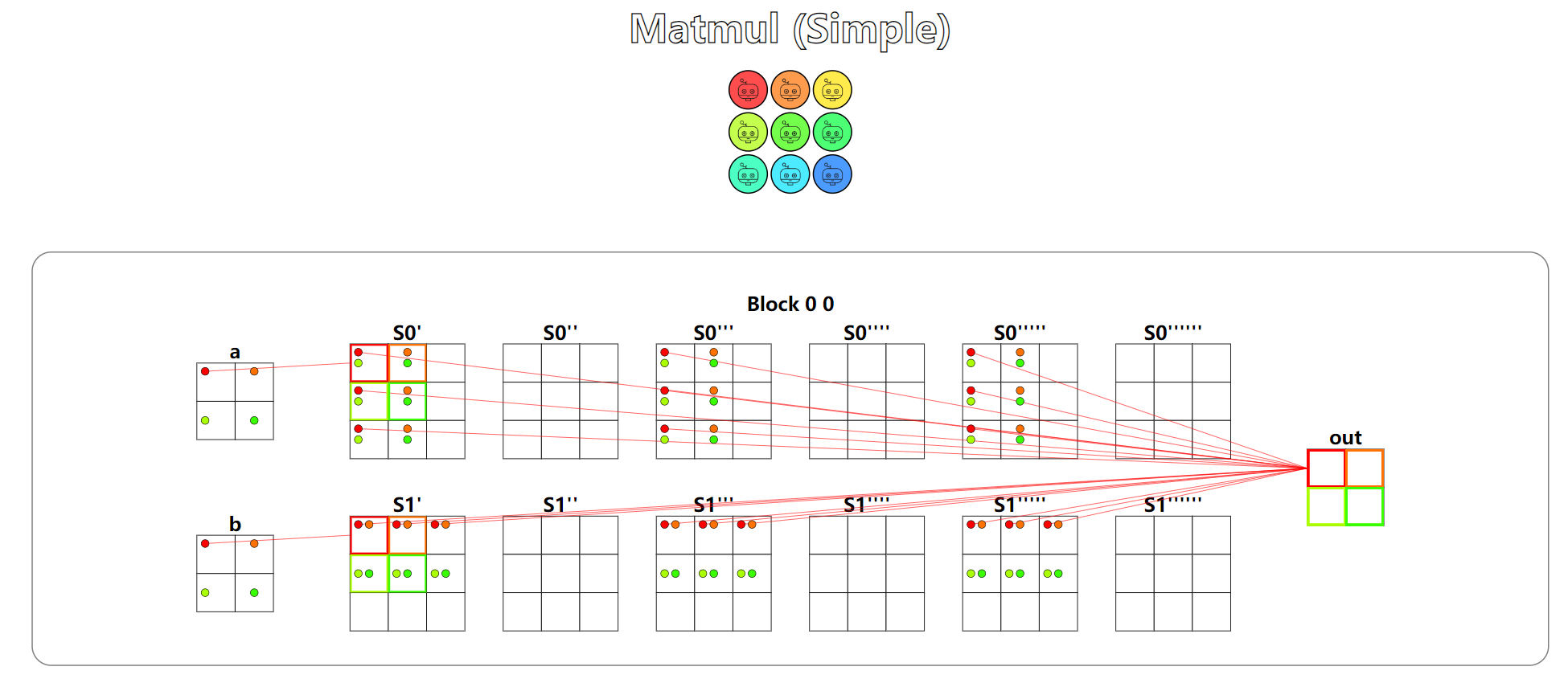
题目：Matrix multiply。矩阵乘法，非常经典的带共享内存版本的矩阵乘法，使用两个共享内存矩阵，用于储存矩阵的局部数据，并在这局部数据上进行矩阵相乘，将结果写到全局内存的输出中。

TPB = 3
def mm_oneblock_test(cuda):
    def call(out, a, b, size: int) -> None:
        a_shared = cuda.shared.array((TPB, TPB), numba.float32)
        b_shared = cuda.shared.array((TPB, TPB), numba.float32)

        i = cuda.blockIdx.x * cuda.blockDim.x + cuda.threadIdx.x
        j = cuda.blockIdx.y * cuda.blockDim.y + cuda.threadIdx.y
        local_i = cuda.threadIdx.x
        local_j = cuda.threadIdx.y
        # Naive，不带共享内存的原始写法
        # if i < size and j < size:
        #     acc = 0
        #     for k in range(size):
        #         acc = acc + a[i, k] * b[k, j]
        #     out[i, j] = acc
        # 带共享内存的写法
        acc = 0
        # 一个Block负责管一个小区域，这个小区域中的元素正好全部能装到Shared memory中
        # 每个Block都加载一次，然后计算Shared memory这一个小矩阵的乘积
        for blockId in range(cuda.blockDim.x):
            # 将当前Block内的数据搬到Shared memory中
            if i < size and (blockId * cuda.blockDim.y + cuda.threadIdx.y) < size:
                a_shared[local_i, local_j] = a[i, blockId * cuda.blockDim.y + cuda.threadIdx.y]
            else:
                # 如果超过原矩阵的边界，则置零，以免上一个Stride中的数据扰乱结果
                a_shared[local_i, local_j] = 0.0
            if j < size and (blockId * cuda.blockDim.x + cuda.threadIdx.x) < size:
                b_shared[local_i, local_j] = b[blockId * cuda.blockDim.x + cuda.threadIdx.x, j]
            else:
                b_shared[local_i, local_j] = 0.0
            # 数据搬完之后，同步一下线程
            cuda.syncthreads()
            # 矩阵乘法，一行乘一列，结果累加
            for k in range(cuda.blockDim.x):
                acc = acc + a_shared[local_i, k] * b_shared[k, local_j]
            cuda.syncthreads()
        # 结果写回
        if i < size and j < size:
            out[i, j] = acc

    return call

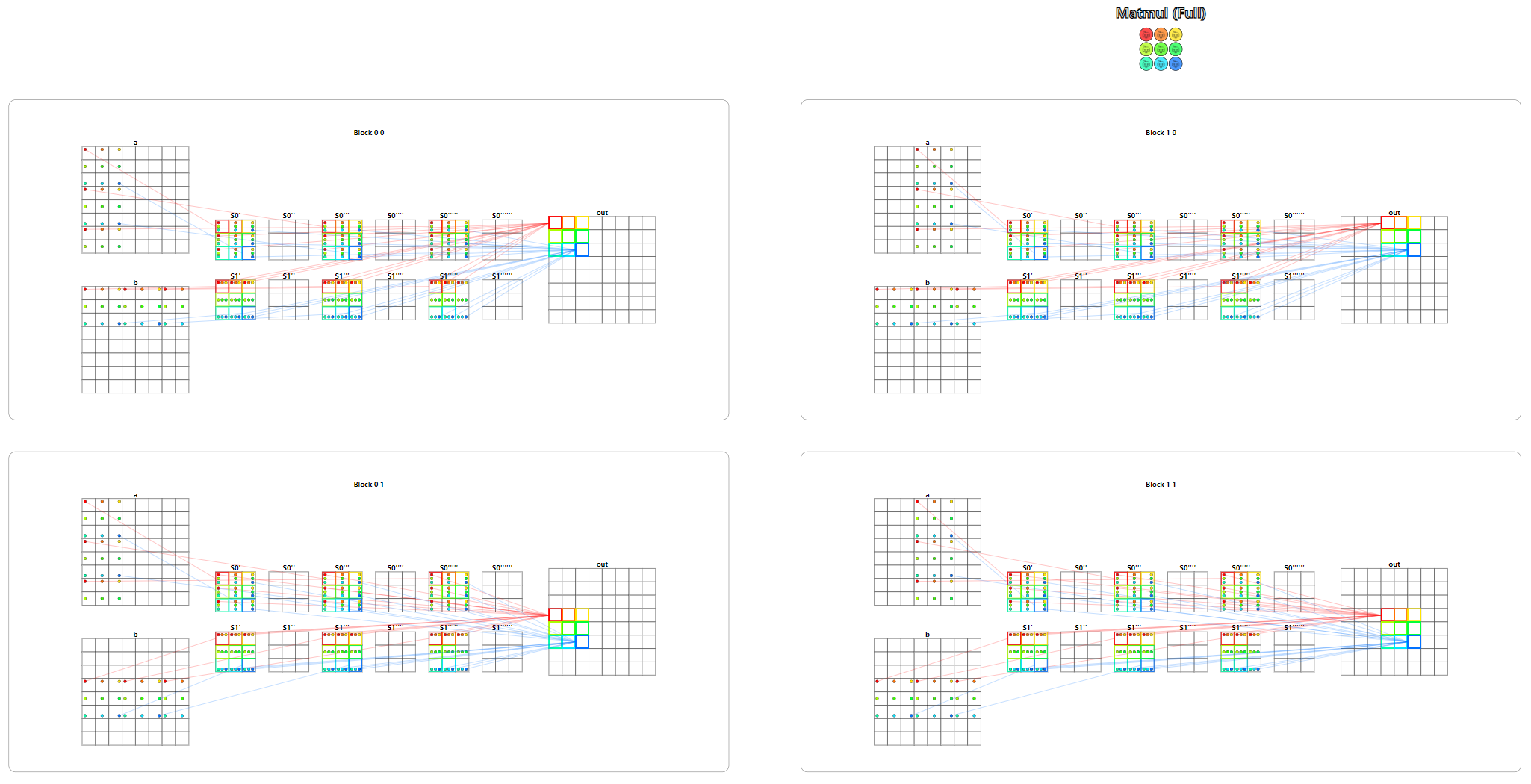
测试用例同样有两个，第一个用例中共享内存的大小比矩阵要大，使用一个Block便可以完成计算。第二个用例中矩阵要大于共享内存的大小，此时就需要分片加载，计算局部矩阵和，最后将结果累加写回到输出。

总结

对于初学者来说，前九题的难度还是十分友好的，第十题开始需要更深入的理解，配合可视化图，花点时间也能完全理解。使用Python编写核函数的方法也降低了学习成本，通过一题之后的小动物视频很有趣。总而言之是一个宝藏小仓库，值得给仓库作者点一个小星星。